Pengantar ke Geometri Fraktal

Geometri fraktal adalah cabang matematika yang mempelajari bentuk-bentuk geometris yang kompleks, tidak teratur, dan sering kali menyerupai pola alam seperti awan, pegunungan, atau salju. Judul bab “Geometri Fraktal: Keajaiban Dimensi Pecahan” menekankan pada aspek ajaib dari fraktal, yaitu kemampuannya untuk memiliki dimensi yang bukan bilangan bulat, melainkan pecahan (seperti 1.26 atau 1.58). Ini berbeda dari geometri Euclidean tradisional, di mana garis memiliki dimensi 1, bidang dimensi 2, dan ruang dimensi 3.

Fraktal pertama kali dipopulerkan oleh Benoit Mandelbrot pada tahun 1970-an, yang menyebutnya sebagai “fraktal” dari kata Latin “frangere” yang berarti “memecah” atau “pecah”. Keajaiban dimensi pecahan ini memungkinkan kita memodelkan fenomena alam yang tampak acak tetapi sebenarnya memiliki pola berulang pada skala berbeda. Dalam bab ini, kita akan menjelajahi definisi, sejarah, konsep matematis, contoh, properti, dan aplikasi fraktal secara rinci dan jelas.

Apa Itu Fraktal?

Fraktal adalah objek geometris yang menunjukkan self-similarity (kesamaan diri), artinya bagian kecil dari objek tersebut mirip dengan keseluruhan objek. Tidak seperti bentuk sederhana seperti lingkaran atau persegi, fraktal memiliki detail tak terbatas: semakin Anda memperbesar, semakin banyak detail yang muncul, dan pola ini berulang selamanya.

Secara formal, fraktal didefinisikan sebagai himpunan yang memiliki dimensi Hausdorff (atau dimensi fraktal) lebih besar dari dimensi topologisnya. Dimensi topologis adalah dimensi intuitif (misalnya, kurva adalah 1-dimensi), sedangkan dimensi Hausdorff mengukur kerumitan dengan mempertimbangkan bagaimana ukuran objek berubah saat diukur pada skala yang lebih halus.

Untuk memahami ini, bayangkan sebuah garis lurus: panjangnya tetap saat diukur dengan penggaris yang lebih kecil. Namun, pada fraktal, “panjang” atau “luas” bertambah tak terbatas saat resolusi meningkat, yang menghasilkan dimensi pecahan.

Sejarah Singkat Geometri Fraktal

Konsep fraktal bukanlah hal baru sepenuhnya. Pada akhir abad ke-19, matematikawan seperti Georg Cantor (himpunan Cantor) dan Helge von Koch (kurva Koch) telah menciptakan objek yang sekarang kita kenal sebagai fraktal, meskipun saat itu dianggap sebagai “monster matematis” karena sifatnya yang paradoksal.

Puncaknya datang pada tahun 1975 ketika Benoit Mandelbrot, seorang matematikawan Polandia-Prancis-Amerika, menerbitkan esai “How Long Is the Coast of Britain?” yang menunjukkan bahwa garis pantai memiliki dimensi pecahan sekitar 1.25 karena kerumitannya. Buku seminalnya, The Fractal Geometry of Nature (1982), memperkenalkan fraktal ke dunia luas, termasuk aplikasi di bidang fisika, biologi, dan seni.

Perkembangan komputer pada 1980-an memungkinkan visualisasi fraktal yang indah, seperti himpunan Mandelbrot, yang menjadi ikon keajaiban matematika.

Konsep Dimensi Pecahan: Bagaimana Menghitungnya?

Dimensi pecahan adalah inti dari keajaiban fraktal. Dalam geometri biasa, dimensi adalah bilangan bulat. Namun, fraktal “mengisi ruang” lebih dari dimensi topologisnya tapi kurang dari dimensi berikutnya.

Metode utama untuk menghitung dimensi fraktal adalah dimensi self-similarity atau dimensi box-counting. Mari kita jelaskan secara rinci.

1. Dimensi Self-Similarity

Untuk fraktal yang dibangun secara iteratif (seperti salju Koch), dimensi $D$D dihitung dengan rumus:

$$D = \frac{\log N}{\log r}$$D=logrlogN​

di mana:

• $N$N adalah jumlah salinan diri yang lebih kecil.
• $r$r adalah faktor pembesaran (scaling factor) untuk membuat salinan tersebut sama dengan keseluruhan.

Contoh sederhana: Bayangkan sebuah garis dibagi menjadi 3 bagian, dan bagian tengah diganti dengan dua garis membentuk segitiga. Ini adalah iterasi pertama kurva Koch.

• $N = 4$N=4 (karena garis asli menjadi 4 segmen lebih kecil).
• $r = 3$r=3 (setiap segmen 1/3 panjang asli).
• Maka $D = \frac{\log 4}{\log 3} \approx 1.2619$D=log3log4​≈1.2619.

Ini berarti kurva Koch memiliki dimensi antara 1 (garis) dan 2 (bidang), mencerminkan kerumitannya yang seperti “mengisi” ruang.

Untuk menghitung ini secara matematis, kita bisa menggunakan logaritma. Misalnya, untuk memverifikasi:

• Hitung $\log 4 = \ln 4 / \ln e \approx 1.3863$log4=ln4/lne≈1.3863
• $\log 3 = \ln 3 / \ln e \approx 1.0986$log3=ln3/lne≈1.0986
• $D = 1.3863 / 1.0986 \approx 1.2619$D=1.3863/1.0986≈1.2619

Ini adalah penjelasan langkah demi langkah: Mulai dari rumus dasar scaling, identifikasi berapa banyak bagian kecil yang dibuat, ukur faktor reduksinya, lalu terapkan logaritma untuk mendapatkan dimensi.

2. Dimensi Box-Counting (atau Minkowski-Bouligand)

Metode ini lebih umum untuk fraktal alami. Bayangkan menutupi objek dengan kotak-kotak berukuran $\epsilon$ϵ. Hitung jumlah kotak yang dibutuhkan $N(\epsilon)$N(ϵ). Dimensi $D$D adalah:

$$D = \lim_{\epsilon \to 0} \frac{\log N(\epsilon)}{\log (1/\epsilon)}$$D=ϵ→0lim​log(1/ϵ)logN(ϵ)​

Ini mengukur bagaimana kerapatan meningkat saat kotak semakin kecil. Untuk garis pantai, semakin kecil $\epsilon$ϵ, semakin banyak detail yang tertangkap, menghasilkan $D > 1$D>1.

Dimensi Hausdorff adalah versi lebih ketat secara matematis, tapi untuk penjelasan dasar, dimensi self-similarity sudah cukup.

Contoh Fraktal Terkenal

Mari kita bahas beberapa contoh klasik untuk mengilustrasikan keajaiban ini. Saya akan sertakan visualisasi untuk kejelasan.

1. Salju Koch (Koch Snowflake)

Ini adalah fraktal yang dibangun dari segitiga sama sisi. Mulai dengan segitiga, lalu pada setiap sisi, tambahkan segitiga kecil di tengah.

• Iterasi 0: Segitiga sederhana (panjang keliling 3, luas terbatas).
• Iterasi 1: Setiap sisi menjadi 4/3 lebih panjang, keliling menjadi tak terbatas setelah iterasi tak hingga, tapi luas tetap terbatas (8/5 kali luas asli).
• Dimensi: $D = \log 4 / \log 3 \approx 1.26$D=log4/log3≈1.26.

nrich.maths.org

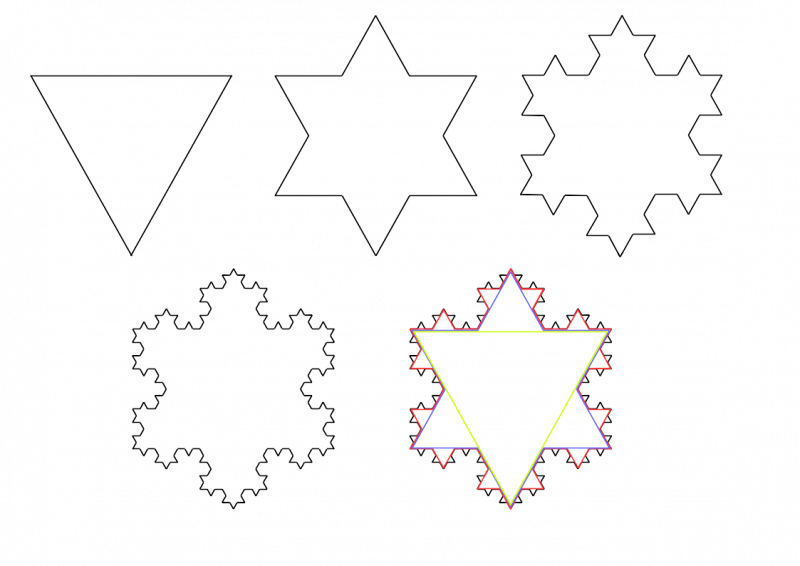
The Koch snowflake | NRICH

Gambar di atas menunjukkan iterasi salju Koch, di mana pola berulang menciptakan bentuk seperti kepingan salju ❄️, dengan detail tak terbatas.

2. Segitiga Sierpinski

Mulai dengan segitiga, hapus segitiga tengah, ulangi pada segitiga tersisa.

• $N = 3$N=3, $r = 2$r=2 (setiap segitiga kecil setengah ukuran).
• Dimensi: $D = \log 3 / \log 2 \approx 1.585$D=log3/log2≈1.585.
• Properti: Luas mendekati nol, tapi “panjang” (ukuran Hausdorff) tak terbatas.

mathigon.org

The Sierpinski Triangle – Fractals – Mathigon

Ini seperti spons yang semakin berlubang, menunjukkan bagaimana fraktal bisa “hilang” dalam ruang tapi tetap kompleks.

3. Himpunan Mandelbrot

Ini adalah fraktal dinamis dari bilangan kompleks. Didefinisikan sebagai himpunan titik $c$c di bidang kompleks di mana iterasi $z_{n+1} = z_n^2 + c$zn+1​=zn2​+c (mulai dari $z_0 = 0$z0​=0) tidak divergen ke tak hingga.

• Dimensi batas: Sekitar 2, tapi dengan detail fraktal.
• Keajaiban: Zoom tak terbatas mengungkap pola baru, seperti mini-Mandelbrot.

en.wikipedia.org

Mandelbrot set – Wikipedia

Gambar ini adalah tampilan keseluruhan himpunan Mandelbrot, sering disebut “sidik jari Tuhan” karena kerumitannya.

4. Himpunan Julia

Mirip Mandelbrot, tapi untuk nilai $c$c tetap. Setiap $c$c menghasilkan Julia set berbeda, sering terhubung atau terpisah seperti debu Cantor.

• Dimensi bervariasi, tapi sering pecahan.

en.wikipedia.org

Julia set – Wikipedia

Contoh ini menunjukkan variasi pola yang indah dari himpunan Julia.

Properti Utama Fraktal

1. Self-Similarity: Bagian mirip keseluruhan, baik eksak (seperti Koch) atau statistik (seperti awan).
2. Rekursi dan Iterasi: Dibangun melalui pengulangan aturan sederhana tak terbatas kali.
3. Non-Integer Dimension: Memungkinkan pemodelan objek nyata yang tidak pas dengan dimensi bulat.
4. Kekacauan dan Ketidakteraturan: Tampak acak, tapi deterministik.
5. Skala Invarian: Sifat sama pada skala berbeda, seperti pohon cabang yang mirip ranting.

Aplikasi Geometri Fraktal

Fraktal bukan hanya teori abstrak; mereka memiliki aplikasi luas:

• Alam dan Sains: Model pegunungan (dimensi ~2.2), sungai, pembuluh darah, atau paru-paru. Di biologi, fraktal menjelaskan pertumbuhan tanaman (L-system).
• Komputer Grafik: Digunakan di film (seperti Star Wars untuk lanskap) dan game untuk tekstur realistis.
• Ekonomi dan Keuangan: Model fluktuasi pasar saham sebagai proses fraktal (multifraktal).
• Medis: Analisis gambar MRI untuk deteksi tumor, karena tumor sering fraktal.
• Seni dan Desain: Seniman seperti Jackson Pollock menciptakan lukisan fraktal; arsitektur menggunakan pola fraktal untuk efisiensi.
• Teknologi: Antena fraktal untuk sinyal lebih baik, kompresi gambar (seperti JPEG menggunakan wavelet fraktal).

Kesimpulan: Keajaiban yang Tak Berakhir

Geometri fraktal membuka pintu ke dunia di mana dimensi bukan lagi kaku, tapi fleksibel seperti alam itu sendiri. Keajaiban dimensi pecahan terletak pada kemampuannya menyatukan kesederhanaan aturan dengan kerumitan tak terbatas, menginspirasi dari matematika murni hingga aplikasi praktis. Jika Anda menyelami lebih dalam, coba buat fraktal sendiri menggunakan software seperti Fractal Explorer atau Python dengan library seperti Matplotlib. Bab ini mengajak kita menghargai bagaimana matematika bisa menangkap keindahan chaos di sekitar kita.